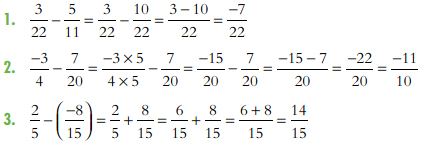Хэрэв өрөөний температур 0-ээс доошбол энэ нь
гэсэн утгатай. Гэвч энэ нь бүхэл тоо ч биш, бутархай тоо биш. Харин үүнийг рационал тоо гэж нэрлэдэг.
Рационал тооны өөр жишээг үзвэл:
Эндээс үзвэл:
- Бүх бүхэл тоонууд рационал тоо байна.
- Бүх бутархай тоонууд ч мөн рационал тоо байна.
- 10-тын тоог 10-тын бутархай хэлбэрээр бичсэн бол мөн рационал тоо байна.
Жишээ нь 0.3, 0.7, 0.25, 0.125 гэсэн 10-тын тоонуудыг 10-тын бутархай хэлбэрт бичвэл тэд рационал тоо болно.
Эквивалент рационал тоо (Equivalent Rational Numbers)
Жишээ ньгэсэн рационал тоог
гэж бичиж болно.
Иймээс 2/3, 4/6, 6/9, 8/12 гэсэн рационал тоонуудыг хоорондоо эквивалент рационал тоонууд гэнэ.
Рационал тооны стандарт хэлбэр (Standard form of a Rational Number)
1. Рационал тоо нь хамгийн энгийн хэлбэртэй байна. Жишээ нь 3/4 гэсэн рационал тоог 15/20 гэж бичихгүй. Үүнтэй адил 1/3 нь хэдийгээр 20/60-тай эквивалент боловч түүнийг 20/60 гэж бичихгүй, харин 1/3 гэж хамгийн энгийн хэлбэрээр бичнэ.
2. Рационал тооны хуваарийг хасах утгатай бичихгүй. Харин хүртвэрийг хасах гэж бичнэ.
3. Мөн рационал тооны хүртвэр болон хуваарийг хоёуланг нь хасах утгатай бичихгүй. Учир нь хуваарь ба хүртвэр нь зэрэг хасах утгатай бол уг рационал тоог нэмэх гэж үзнэ.
Рационал тоог тоон шугам дээр дүрслэх (Representation of a Rational Number on the Number Line)
Жишээ нь 3/2 нь 3 хүртэлх утгын хагас юм. Харин -3/2 нь 0-ээс зүүн тийш, 3/2 нь 0-ээс баруун тийш гэсэн утгатай
Рационал тоонуудыг харьцуулах (Comparison of Rational Numbers)
- Нэмэх рационал тоо хасах рационал тооноос үргэлж их байна. Жишээ нь 1/2 > -3/2; 3/4 > -50/4
- Тэг нь ямар ч нэмэх рационал тооноос бага, хасах рационал тооноос их байна. Жишээ нь -3/4 < 0 < 3/4; -10 < 0 < 1/2
- Харин нэмэх рационал тоонуудыг харьцуулах нь бутархай тоог харьцуулахтай адилхан.
- Харин хасах рационал тоонуудыг харьцуулахдаа нэмэх утгуудыг нь харьцуулаад эсрэгээр нь авна. Жишээ нь -3/4 ба -1/2-ийг харьцуулах бол эхлээд 3/4 ба 1/2-ийг бутархай тоог хэрхэн харьцуулдаг аргаар харьцуулна. Ингэхэд 3/4 > 1/2 байна. Хасах тооны хувьд энэ нь эсрэгээрээ байх буюу -3/4 < -1/2 байна.
2 рационал тооны хооронд рационал тоо нэмэх (Inserting Rational Numbers Between Two Given Rational Numbers)
10 ба 15 гэсэн 2 бүхэл тооны хооронд 11, 12, 13, 14 гэсэн 4 бүхэл тоо байна. -9 ба -5 гэсэн бүхэл тооны хооронд -8, -7, -6 гэсэн 3 тоо байна.
Харин 2 рационал тооны хооронд байж болох рационал тоо нь хязгааргүй олон байна.
1/2 ба 1/5 гэсэн 2 рационал тоог авч үзье. Тэгвэл 1/2-ийг 5/10, харин 1/5-ийг 2/10 гэж эквивалент утгаар сольж ижил хуваарьтай болгож болно.
Тэгвэл 2/10 ба 5/10 гэсэн 2 рационал тооны хооронд 3/10, 4/10 гэсэн 2 рационал тоо байна.
3/10 ба 4/10-ийг ижилхэн 100 гэсэн хуваарьтай болгох юм бол 30/100 ба 40/100 гэсэн эквивалент утгатай байна.
Тэгвэл 30/100 ба 40/100 рационал тооны хооронд 31/100, 32/100, 33/100 ... 38/100, 39/100 рационал тоонуудыг нэмж болно. Ийм аргаар хэчнээн ч рационал тоонуудыг нэмж оруулж болно.
Рационал тоонуудыг нэмэх (Addition of Rational Numbers)
Ижил хуваарьтай рационал тоонуудыг хооронд нь шууд нэмнэ.
Харин ижил бус хуваарьтай бол тэднийг эхлээд ижил хуваарьтай болгоно.
3/4-ийн хуваарь нь 4 бол -5/8-ийн хуваарь 8 байна. Иймээс 4 ба 8-ийн ХБЕХ буюу LCM нь 8 байна. Ингээд 3/4-г 8 хуваарьтай болговол хуваарь хүртвэрийг 2-уланг нь 2-оор үржиж 3/4 = 6/8 болно.
Үүнтэй адил 5/12 дээр -7/18-ийг нэмэх юм бол 12 ба 18-ийн ХБЕХ буюу LCM нь 36 байх тул 2-уланг нь 36 хуваарьтай болгоод хооронд нь нэмнэ.
Рационал тоонуудын хувьд хасах үйлдэл нь нэмэх үйлдэлтэйгээ адилхан хийгдэнэ. Жишээ нь:
Рационал тоонуудыг үржих (Multiplication of Rational Numbers)
- Хүртвэрүүдийг үржүүлж үржвэрийг нь хүртвэрт тавина.
- Хуваариудыг үржүүлж үржвэрийг нь хуваарьт тавина.
- Рационал тоог энгийн хэлбэрт шилжүүлнэ.
Рационал тоонуудыг хуваах (Division of Rational Numbers)
